What is Microscope Resolution?

Microscope resolution is the amount of detail that can be resolved from the light being refracted through a specimen and presented to the observer through a microscope. Resolution can also be thought of as the minimum distance between two distinct points that can be distinguished by the observer.

For example, imagine you had plant specimen on your slide under your microscope for examination and when you look at two plant cells side by side unresolved they just look like a blurry mass but when you focus the microscope they now become clear and you can clearly distinguish one cell from another.

When I first started microscopy, this was a little ambiguous to me and really did not add much to my understanding of the concept of resolution and what it means. So I dug a little deeper and it turns out there is much more to the story.

In this article we will look at some of the fundamentals that will help you understand the concept of resolution in the context of microscopy and hopefully present it to you in a concise digestible manner.

Wave Optics

To understand resolution, we need to understand wave optics. Christiaan Huygens was a Dutch inventor, mathematician, physicist, and astronomer that lived from 1629 to 1695 and is credited with the idea that light travels in waves, not in lines like you might expect after playing around with a laser pointer.

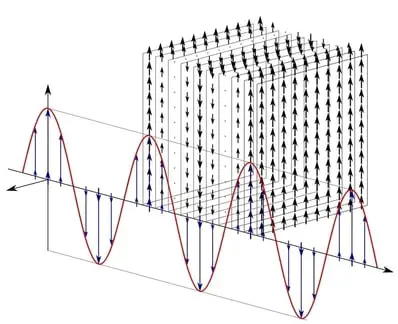
Huygens postulated that there are two types of waves, plane waves and spherical waves. You can think of plane waves as a front of light moving in a straight direction with light waves traveling one right after the other. The image below will give you a sense of what a plane wave looks like but don’t worry too much about it if you’re not quite getting it.

A spherical wave is where you have waves that are either converging to a point or diverging from a point. Spherical waves have the curvature of a sphere which is where it gets the name. Again, hang in there if you’re not quite following.

Spherical wave either converging to a point or diverging from a point

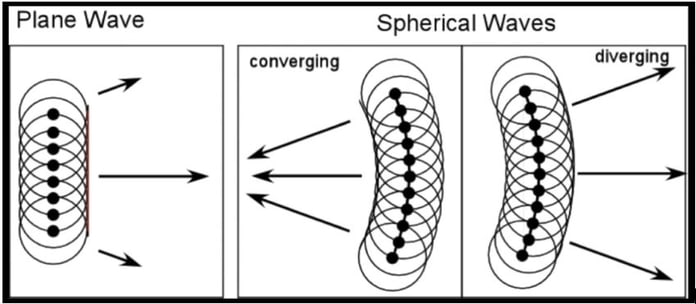
According to Huygens both of these waves are made up of elemental parts called wavelets. Wavelets are little points of light that distribute light in all directions. Below is a drawing that illustrates how a plane wave a spherical wave is just a series of wavelets. In the plane wave they are moving in a straight direction and in a spherical wave they are converging and diverging.

The reason this was necessary to understand these building blocks is because this gets us to the concept of diffraction. If you have an extremely small hole or opening and you have a plane wave behind that hole trying to escape, you may only have a few wavelets that get through and that wavelet gets through and spreads light in all directions. This diffraction phenomenon is explaining why light seems to bend in all directions.

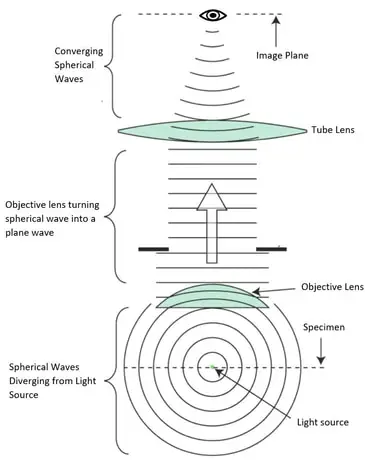
Not let’s put this in the context of a microscope. A microscope works by shining light up through a specimen and at this point, before the light reaches the objective lens it is in a divergent spherical state. The objective lens transforms the spherical wave into a plane wave. The tube lens transforms the wave back into a spherical wave but this time converging into a point.

A higher numerical aperture objective will be able to capture more of this wavelet than a lower numerical aperture. We discuss numerical aperture further in the next section. So, if the wavelet contains the imaging information that is being shone through the specimen you can now start to see what is meant by resolution.

Numerical Aperture

Numerical aperture is just a way of expressing the ability of an objective lens to gather light information, which is really information about our specimen, and resolve details at some given working distance. If you remember, the way a microscope works is light shines up from a light source, through a condenser lens, through a hole is in the stage, through the slide, and through the small holes and the surroundings of the specimen and diffracts the light which ends up making an upside down cone of light. The degree to which the objective lens can capture or gather this light is really what we are talking about with numerical aperture.

Numerical aperture is expressed by performing a calculation on this cone of light. The formula for this calculation is the following.

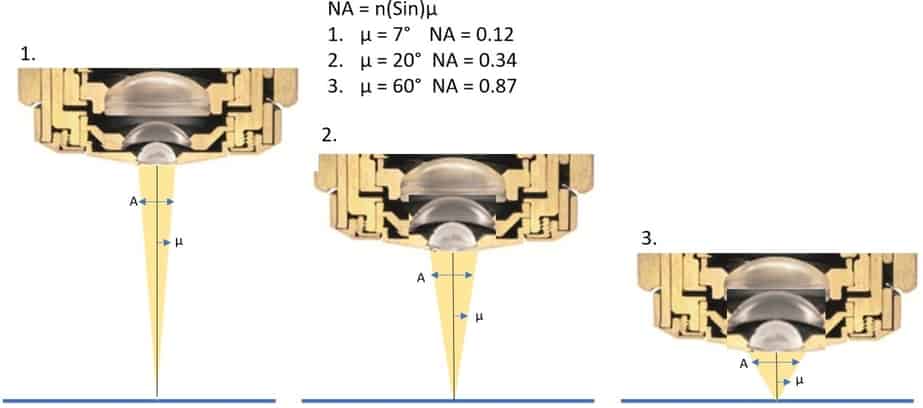
Numerical Aperture (NA) = n(sin µ)

Let’s break this formula down a bit. The µ variable is just half of the angular aperture A as shown in the diagram below. So, the cone obviously will have an angle that we can calculate to get µ all we need to do is divide that angle by 2.

The variable n is the refractive index of the of the medium between objective lens and the slide cover over the specimen. Medium just means whatever the light has to travel through. The baseline is air and air has a refractive index of 1.00. You can achieve values higher than one if you use mediums like immersion oil. When you use immersion oil the objective lens actually comes into contact with the oil that is sitting on the slide cover, so less light is refracted away. For more on oil immersion see this post.

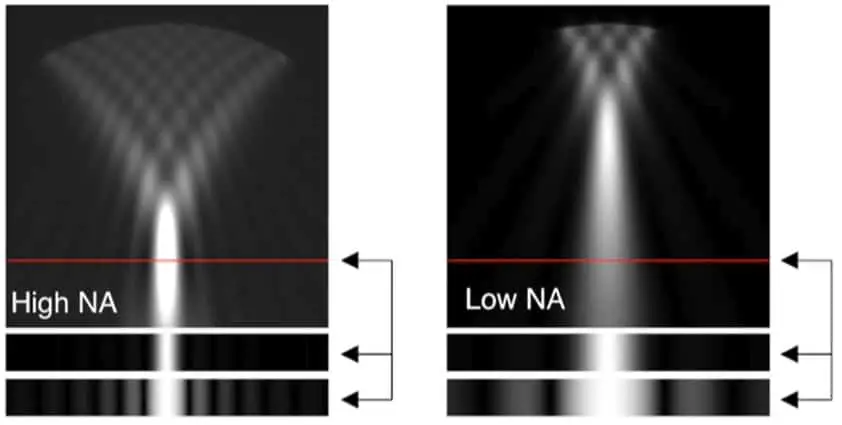
To close out this point, the image to the right shows wavelet spread on a high numerical aperture on the left and wavelet spread on a low numerical aperture on the right. As you can see the objective with the higher numerical aperture is clearly able to give us more detail with separation between the wavelets.

Wavlets with high and low numerical aperture

Airy Disk

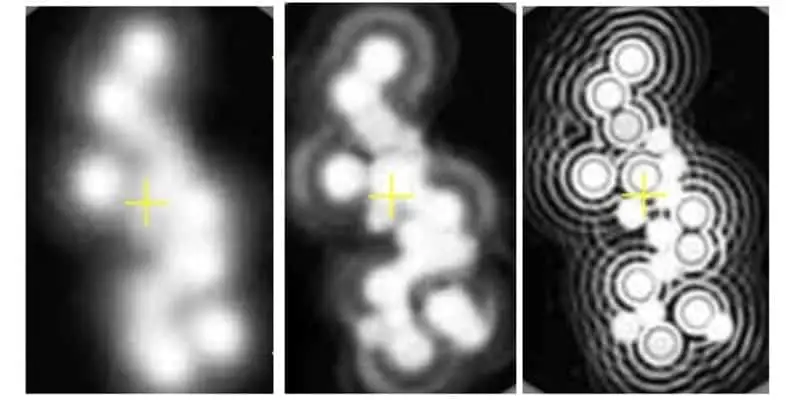
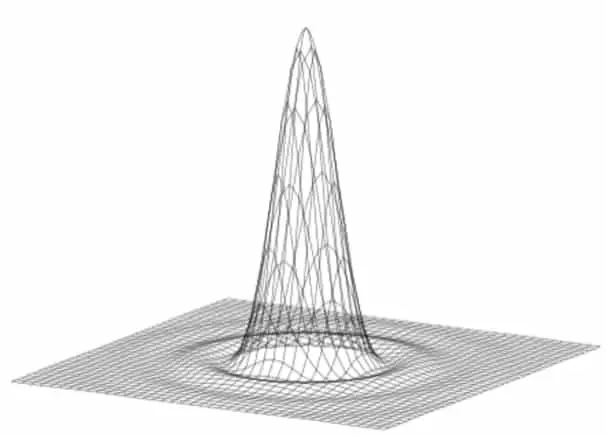
As we have seen, as light passes up through a specimen and gets transformed into an image. The points of the specimen are seen as small patterns. These patterns are called Airy patterns and the central maximum of the Airy patterns is called an Airy disk. The disks visually looks like concentric light and dark circles.

This is where we get back to our original definition of resolution being the minimum distance two distinct points that can be distinguished between two points; the points being the Airy disks. As you can see in the image below as we move from left to right, we are able to resolve distinct points. This limit where we are able to distinguish two objects as separate entities can be measured as resolution.

The Airy Disk idea is credited to George Biddell Airy who lived from 1801 – 1892. Airy was an English astronomer and mathematician. Airy’s paper ‘On the Diffraction of an Object-Glass with Circular Aperture’ is where Airy expounded on these ideas.

Rayleigh Criterion

I’ll spare you the math, but the Rayleigh criterion builds on the Airy disk concept and is basically a mathematical criterion for when two points are distinguishable from one another.

Now that you understand Airy disks, the Raleigh criterion, and numerical aperture, you can probably guess that if we can get smaller Airy disks, we can discern more detail or achieve more resolution. It turns out that there is an inverse relationship between numerical aperture and Airy disks such that as the as the numerical aperture increases and more light information is collected the Airy disks are smaller.

Putting it All Together

If you’ve read other articles on numerical aperture and magnification, you may be wondering how does resolution depend on the wavelength of light, refractive index, and numerical aperture? Also, you may be wondering how are resolution and magnification related? Let’s tackle the first question.

Lets first remember that resolution is defined as the shortest distance between two points that can still be resolved. This distance is measured is micrometers. So, let’s take the formula for resolution and break it down.

The formula for Resolution is:

r = λ/(2NA)

Where r is resolution λ is wavelength NA is the numerical aperture. We know from the numerical aperture article that the numerical aperture of the condenser and of the objective lens should match so we multiply it by 2.

Remember that the formula for numerical aperture is:

NA = (n) sin(µ)

Where n is the refractive index of the medium through which observation is occurring and we are taking the sin of µ which is half of the angular aperture of the cone of light. If you are observing something without oil your refractive index will be approximately 1. So, we can re-write the formula for resolution as:

R = λ / 2((n) sin(µ))

So you can see that we can change the value of the wavelength by using color filters which will change the number in the numerator of the equation and we can change the numerical aperture and refractive index values in the denominator by changing the objective lens and using oil immersion. This will give us different values for resolution.

I hope this illustrates the relationship between wavelength of light, refractive index and numerical aperture.

Now for the second question ‘how are resolution and magnification related?’

Now that we have resolution, which gives a value in micrometers, we know the shortest distance between two points of the specimen. The problem is that if that distance is too small our eyes cannot distinguish any separation which manifests as a blurry image. So, for any magnification level there is a limit to the resolution that you can achieve based again on the factors that are used to compute resolution.

It turns out that the minimum magnification for visual observation is about 500 multiplied by the numerical aperture of the objective lens and the maximum is 1000 multiplied by the numerical aperture of the objective lens. For a chart that clearly shows this see Microscope Magnification: Explained.

Takeaways

Resolution seems like such a simple thing considering how its used in everyday language but as you have seen, in microscopy there are multiple concepts in optics and physics that that contribute to the concept of resolution. The resolving power of a microscope is the ability to resolve the very minute details in a specimen and in this article, we have seen the physics and mechanics of this process in action.